El cálculo diferencial es una parte del análisis matemático que consiste en el estudio de cómo cambian las funciones cuando sus variables cambian. El principal objeto de estudio en el cálculo diferencial es la derivada. Una noción estrechamente relacionada es la de diferencial de una función. El estudio del cambio de una función es de especial interés para el cálculo diferencial, en concreto el caso en el que el cambio de las variables es infinitesimal.
lunes, 19 de octubre de 2015
Temario
Unidad 3 Límites y Continuidad
3.1 Límite de una Sucesión
3.2 Límite de una función de variable real
3.3 Cálculo de Límites
3.4 Propiedades de los Límites
3.5 Límites Laterales
3.6 Límites Infinitos Límites al Infinito
3.7 Asíntotas
3.8 Funciones Continuas y Discontinuas en un punto y en un Intervalo
3.9 Tipos de Discontinuidades
3.1 Límite de una Sucesión
El límite de una sucesión es uno de los conceptos más antiguos del análisis matemático. Este concepto está estrechamente ligado al de convergencia, una sucesión de elementos de un conjunto es convergente si y solo si en el mismo conjunto existe un elemento (al que se le conoce como límite) al cual la sucesión se aproxima tanto como se desee a partir de un momento dado. Si una sucesión tiene límite, se dice que es una sucesión convergente, y que la sucesión converge o tiende al límite. En caso contrario, la sucesión es divergente.
La definición significa que eventualmente todos los elementos de la sucesión se aproximan tanto como queramos al valor límite. La condición que impone que los elementos se encuentren arbitrariamente cercanos a los elementos subsiguientes no implica, en general, que la sucesión tenga un límite.
Qué se entiende por próximo da lugar a distintas definiciones de límite dependiendo del conjunto donde se ha definido la sucesión



 .
.
 o bien
o bien ![x_n \xrightarrow[{\;\; n \to \infty\;\; }]{}l](https://upload.wikimedia.org/math/5/2/3/5234b680d84cda5b991c41114787b44f.png)
La definición significa que eventualmente todos los elementos de la sucesión se aproximan tanto como queramos al valor límite. La condición que impone que los elementos se encuentren arbitrariamente cercanos a los elementos subsiguientes no implica, en general, que la sucesión tenga un límite.
Qué se entiende por próximo da lugar a distintas definiciones de límite dependiendo del conjunto donde se ha definido la sucesión



El término general de una sucesión  tiene límite
tiene límite  , cuando
, cuando 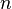 tiende a
tiende a  , si para todo valor
, si para todo valor  por pequeño que sea, existe un valor
por pequeño que sea, existe un valor  a partir del cual si
a partir del cual si  tenemos que la distancia de
tenemos que la distancia de  a
a  es menor que
es menor que  , es decir:
, es decir:
 tiene límite
tiene límite  , cuando
, cuando 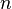 tiende a
tiende a  , si para todo valor
, si para todo valor  por pequeño que sea, existe un valor
por pequeño que sea, existe un valor  a partir del cual si
a partir del cual si  tenemos que la distancia de
tenemos que la distancia de  a
a  es menor que
es menor que  , es decir:
, es decir: .
.Notación
 o bien
o bien ![x_n \xrightarrow[{\;\; n \to \infty\;\; }]{}l](https://upload.wikimedia.org/math/5/2/3/5234b680d84cda5b991c41114787b44f.png)
o también
o simplemente
Ejemplos
- La sucesión 1/1, 1/2, 1/3, 1/4, ... converge al límite 0.
- La sucesión 1, -1, 1, -1, 1, ... es oscilante.
- La sucesión 1/2, 1/2 + 1/4, 1/2 + 1/4 + 1/8, 1/2 + 1/4 + 1/8 + 1/16, ... converge al límite 1.
- Si a es un número real con valor absoluto |a| < 1, entonces la sucesión an posee límite 0. Si 0 < a ≤ 1, entonces la sucesión a1/n posee límite 1.



Límite de una sucesión compleja
Se dice que la sucesión converge hacia un complejo 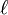 si y solo si
si y solo si
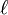 si y solo si
si y solo si
Nótese que es la misma definición que para  , con módulo en lugar del valor absoluto.
, con módulo en lugar del valor absoluto.
 , con módulo en lugar del valor absoluto.
, con módulo en lugar del valor absoluto.
Se puede escribir
 o más simplemente, si no hay ambigüedad
o más simplemente, si no hay ambigüedad 
Las sucesiones complejas convergentes poseen las mismas propiedades que las sucesiones reales, excepto las de relación de orden: el límite es único, una sucesión convergente tiene módulo acotado, toda sucesión de Cauchy converge (en efecto,  es también completo).
es también completo).
 es también completo).
es también completo).Ejemplos
Convergencia puntual
El concepto de convergencia puntual es uno de los varios sentidos en los cuales una sucesión de funciones puede converger a una función particular.
Una sucesión de funciones  definidas en un conjunto no vacío
definidas en un conjunto no vacío 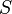 con valores en un espacio métrico
con valores en un espacio métrico  converge puntualmente a una función
converge puntualmente a una función  si
si
 definidas en un conjunto no vacío
definidas en un conjunto no vacío 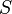 con valores en un espacio métrico
con valores en un espacio métrico  converge puntualmente a una función
converge puntualmente a una función  si
si
para cada  fijo. Esto significa que
fijo. Esto significa que
 fijo. Esto significa que
fijo. Esto significa que(5)
La sucesión de funciones  con
con ![x\in [0,1]](https://upload.wikimedia.org/math/c/6/2/c628ba2b1047de93f66cb815d986e107.png) converge puntualmente a la función
converge puntualmente a la función  puesto que
puesto que
 con
con ![x\in [0,1]](https://upload.wikimedia.org/math/c/6/2/c628ba2b1047de93f66cb815d986e107.png) converge puntualmente a la función
converge puntualmente a la función  puesto que
puesto que
para cada ![x\in [0,1]](https://upload.wikimedia.org/math/c/6/2/c628ba2b1047de93f66cb815d986e107.png) fijo.
fijo.
![x\in [0,1]](https://upload.wikimedia.org/math/c/6/2/c628ba2b1047de93f66cb815d986e107.png) fijo.
fijo.Convergencia uniforme
Una sucesión de funciones  definidas en un conjunto no vacío
definidas en un conjunto no vacío 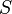 con valores en un espacio métrico
con valores en un espacio métrico  converge uniformemente a una función
converge uniformemente a una función  si para todo
si para todo 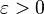 existe un entero
existe un entero 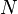 (que depende de
(que depende de  ) tal que
) tal que
 definidas en un conjunto no vacío
definidas en un conjunto no vacío 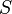 con valores en un espacio métrico
con valores en un espacio métrico  converge uniformemente a una función
converge uniformemente a una función  si para todo
si para todo 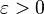 existe un entero
existe un entero 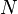 (que depende de
(que depende de  ) tal que
) tal que
para todo  y todo
y todo  . Es decir,
. Es decir,
 y todo
y todo  . Es decir,
. Es decir,(6)
El concepto de convergencia uniforme es un concepto más fuerte que el de convergencia puntual. En (5), 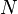 puede depender de
puede depender de  y de
y de  mientras que en (6),
mientras que en (6), 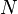 sólopuede depender de
sólopuede depender de  . Así, toda sucesión que converge uniformemente, converge puntualmente. El enunciado recíproco es falso, y un contraejemplo clásico lo constituyen las sucesión de funciones
. Así, toda sucesión que converge uniformemente, converge puntualmente. El enunciado recíproco es falso, y un contraejemplo clásico lo constituyen las sucesión de funciones ![f_n:[0,1]\to \mathbb R](https://upload.wikimedia.org/math/9/e/2/9e277977259edf367a0c03421540ce45.png) definidas por
definidas por  . Esta sucesión converge puntualmente a la función
. Esta sucesión converge puntualmente a la función
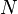 puede depender de
puede depender de  y de
y de  mientras que en (6),
mientras que en (6), 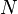 sólopuede depender de
sólopuede depender de  . Así, toda sucesión que converge uniformemente, converge puntualmente. El enunciado recíproco es falso, y un contraejemplo clásico lo constituyen las sucesión de funciones
. Así, toda sucesión que converge uniformemente, converge puntualmente. El enunciado recíproco es falso, y un contraejemplo clásico lo constituyen las sucesión de funciones ![f_n:[0,1]\to \mathbb R](https://upload.wikimedia.org/math/9/e/2/9e277977259edf367a0c03421540ce45.png) definidas por
definidas por  . Esta sucesión converge puntualmente a la función
. Esta sucesión converge puntualmente a la función
ya que
mientras que  Sin embargo esta sucesión no converge uniformemente, pues para
Sin embargo esta sucesión no converge uniformemente, pues para  no existe un
no existe un 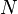 que satisfaga (6).
que satisfaga (6).
 Sin embargo esta sucesión no converge uniformemente, pues para
Sin embargo esta sucesión no converge uniformemente, pues para  no existe un
no existe un 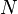 que satisfaga (6).
que satisfaga (6).
De especial interés es el espacio de las funciones continuas  definidas sobre un compacto
definidas sobre un compacto  En este caso, una sucesión de funciones
En este caso, una sucesión de funciones  converge uniformemente a una función
converge uniformemente a una función  si, y sólo si, converge en la norma del sup, i.e.,
si, y sólo si, converge en la norma del sup, i.e.,
 definidas sobre un compacto
definidas sobre un compacto  En este caso, una sucesión de funciones
En este caso, una sucesión de funciones  converge uniformemente a una función
converge uniformemente a una función  si, y sólo si, converge en la norma del sup, i.e.,
si, y sólo si, converge en la norma del sup, i.e.,Sucesiones en otros espacios matemáticos
Una sucesión de elementos  de un espacio métrico
de un espacio métrico  converge a un elemento
converge a un elemento 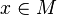 si para todo número
si para todo número  existe un entero positivo
existe un entero positivo 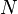 (que depende de
(que depende de ) tal que
) tal que
 de un espacio métrico
de un espacio métrico  converge a un elemento
converge a un elemento 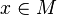 si para todo número
si para todo número  existe un entero positivo
existe un entero positivo 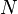 (que depende de
(que depende de ) tal que
) tal que(1)
Intuitivamente, esto significa que los elementos  de la sucesión se pueden hacer arbitrariamente cercanos a
de la sucesión se pueden hacer arbitrariamente cercanos a  si
si  es suficientemente grande, ya que
es suficientemente grande, ya que  determinala distancia entre
determinala distancia entre  y
y  . A partir de la definición es posible demostrar que si una sucesión converge, lo hace hacia un único límite.
. A partir de la definición es posible demostrar que si una sucesión converge, lo hace hacia un único límite.
 de la sucesión se pueden hacer arbitrariamente cercanos a
de la sucesión se pueden hacer arbitrariamente cercanos a  si
si  es suficientemente grande, ya que
es suficientemente grande, ya que  determinala distancia entre
determinala distancia entre  y
y  . A partir de la definición es posible demostrar que si una sucesión converge, lo hace hacia un único límite.
. A partir de la definición es posible demostrar que si una sucesión converge, lo hace hacia un único límite.
La definición se aplica en particular a los espacios vectoriales normados y a los espacios con producto interno. En el caso de un espacio normado  la norma
la norma  induce la métrica
induce la métrica  para cada
para cada  ; en el caso de un espacio con producto interno
; en el caso de un espacio con producto interno  el producto interno
el producto interno 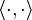 induce la norma
induce la norma  para cada
para cada 
 la norma
la norma  induce la métrica
induce la métrica  para cada
para cada  ; en el caso de un espacio con producto interno
; en el caso de un espacio con producto interno  el producto interno
el producto interno 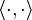 induce la norma
induce la norma  para cada
para cada 
Suscribirse a:
Entradas (Atom)








